Resistors in Parallel: Concepts, Calculations, and Real-World Applications

Description:

In a parallel network of resistors, all the resistors are connected across the same potential difference, which is not the case in a series combination.
The current can take more than one path in a parallel network. As the current flows through multiple paths, it is not the same for all branches, unlike in series networks.
Resistors in a parallel combination have a common voltage, and hence, the voltage drop across each resistor is the same as the total voltage applied across them.

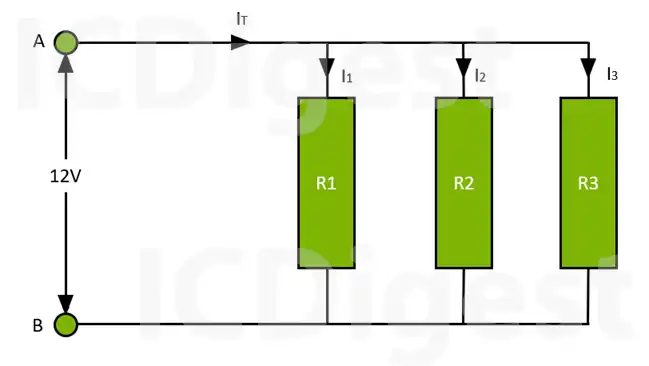
V_R1= V_R2= V_R3= 12V

As seen in the series network, the total resistance in the circuit was the sum of all the resistances present in the circuit.
In a parallel combination, the method for calculating the total equivalent resistance is a bit different.
Let’s see the method to calculate the total resistance acting in a parallel network, given above in the figure.

$$\;\frac{1}{RT}\;=\;\frac{1}{R1}\;+\;\frac{1}{R2}\;+\;\frac{1}{R3}\;……..\;\frac{1}{Rn}\;$$

Parallel Resistance gives us a value known as Conductance (G).
The unit of conductance is Siemens (S). Conductance is the reciprocal of resistance
(G = 1/R).
The equation of Total Conductance in a Parallel Network is similar to a series resistive network:
G_T= G₁+ G₂+ G₃ ……. + G_n
We now know that parallel networks are those that are connected between the same two points.
But a parallel resistive network can take many forms, which won’t catch our eye as a “parallel network”.

Some of the examples of how resistors can be connected in parallel are given here.

Let us now see an example of how to calculate the total resistance in a parallel network for a better understanding.

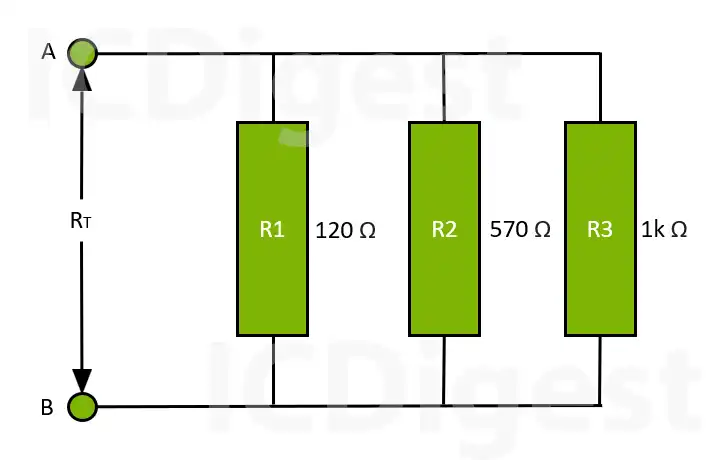
Find the total resistance, R_T of the following resistors connected in a parallel network.

The total resistance R_T across the two terminals A and B is calculated as:

$$\;\frac{1}{RT}\;=\;\frac{1}{R1}\;+\;\frac{1}{R2}\;+\;\frac{1}{R3}\;$$

$$\;\frac{1}{RT}\;=\;\frac{1}{120}\;+\;\frac{1}{570}\;+\;\frac{1}{1000}\;\;=\;0.0110$$

$$\;RT=\;\frac{1}{0.0110}\;=\;90.90Ω$$

If only 2 resistors are connected in a circuit, then a simpler way to calculate their total resistance is given by the following formula:

$$\;RT\;=\;\frac{R1*R2}{R1+R2}\;$$

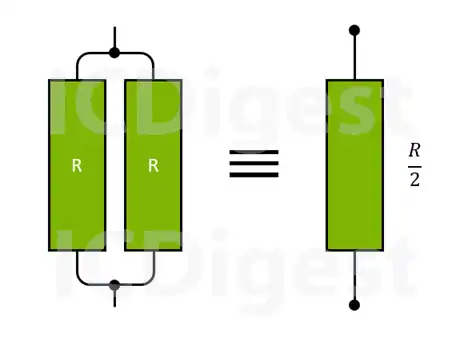
When two resistances or impedances are connected in parallel and have the same value, the total or equivalent resistance, RT, will be half the value of one of the resistors, which is R/2.
Similarly, for three identical resistors in parallel, the equivalent resistance will be R/3, and so on.